El pasado 27 de julio la revista Nature Communications publicaba un artículo con un gran impacto mediático internacional sobre la manera en la que el tejido epitelial (o epitelio) se organiza para conformar y recubrir las cavidades y las superficies estructurales del cuerpo de los animales a medida que éstos se van desarrollando.
La imagen muestra un ejemplo de epitelio cilíndrico o columnar: (https://es.wikipedia.org/wiki/Epitelio#/media/File:Simple_columnar_epithelium_tissue.svg )
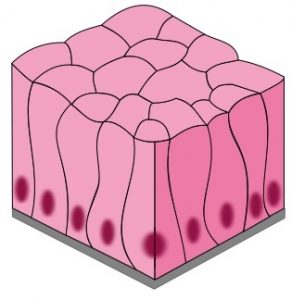 Lo excepcional del trabajo, aparentemente técnico a partir de esta descripción, radica, por una parte, en su dificultad (las estructuras tridimensionales en las que se van acoplando han sido hasta el momento prácticamente un misterio; se observa que suceden, pero no cómo); por otra, en que la posible explicación que se aporta ha sido realizada mediante modelos y razonamientos matemáticos; y finalmente, en que la ha desarrollado un grupo de investigadores españoles, de la Universidad de Sevilla concretamente.
Lo excepcional del trabajo, aparentemente técnico a partir de esta descripción, radica, por una parte, en su dificultad (las estructuras tridimensionales en las que se van acoplando han sido hasta el momento prácticamente un misterio; se observa que suceden, pero no cómo); por otra, en que la posible explicación que se aporta ha sido realizada mediante modelos y razonamientos matemáticos; y finalmente, en que la ha desarrollado un grupo de investigadores españoles, de la Universidad de Sevilla concretamente.
Próximos a la inauguración de la sala de matemáticas del Museo de la Ciencia de Valladolid, encontramos con este trabajo una razón más para mostrar la importancia de las matemáticas en la ciencia y nuestra vida cotidiana. Prácticamente todos están convencidos de que esta disciplina proporciona el lenguaje riguroso y formal de la ciencia, pero hay aún muchas personas que creen que todo en ellas está ya inventado, que, salvo una serie de resultados totalmente teóricos, casi filosóficos, y sin aplicación práctica alguna, está todo ya dicho, descubierto y explotado. Y nada más lejos de la realidad.
Y para muestra este botón. ¿Qué puede haber más cerrado que los cuerpos geométricos que estudiamos en la escuela? Prismas, pirámides, poliedros, cilindros, conos, esferas,… nos los sabemos todos. ¿Seguro? Pues les presentamos, gracias a este trabajo, un nuevo tipo: los escutoides.
En la imagen (https://es.wikipedia.org/wiki/Escutoide#/media/File:Prism, frustum,_prismatoid_and_scutoid_es.svg)
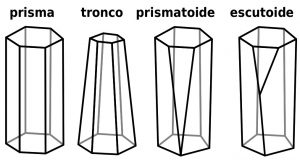 podemos ver diferentes posibilidades de unir superficies paralelas (por ejemplo, dos hexágonos) mediante segmentos. Si estos son paralelos y perpendiculares en los vértices a las bases, tenemos los conocidos prismas (primer dibujo). Si los segmentos forman cierto ángulo, son troncos de pirámide (segundo dibujo). En ambos casos los hay rectos y oblicuos, pero vayamos al caso más general. Los prismatoides son poliedros cuyos vértices se encuentran también en dos planos paralelos, pero cuyas caras laterales son trapezoides o triángulos. En el caso del tercer dibujo vemos un prismatoide en el que la base superior es un hexágono y la inferior un pentágono.
podemos ver diferentes posibilidades de unir superficies paralelas (por ejemplo, dos hexágonos) mediante segmentos. Si estos son paralelos y perpendiculares en los vértices a las bases, tenemos los conocidos prismas (primer dibujo). Si los segmentos forman cierto ángulo, son troncos de pirámide (segundo dibujo). En ambos casos los hay rectos y oblicuos, pero vayamos al caso más general. Los prismatoides son poliedros cuyos vértices se encuentran también en dos planos paralelos, pero cuyas caras laterales son trapezoides o triángulos. En el caso del tercer dibujo vemos un prismatoide en el que la base superior es un hexágono y la inferior un pentágono.
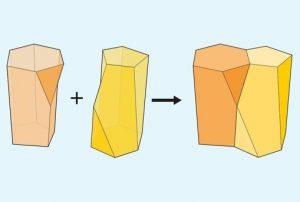
En el nuevo cuerpo, el escutoide, entre los trapezoides de dos caras contiguas, aparece un triángulo, que se ha formado al generar una “y griega” a partir del punto medio de la arista común. Ese triángulo es precisamente el que da nombre al objeto, ya que recuerda a la disposición de dos regiones del tórax de algunos insectos: el scutum (escudo) y el scutellum. Y, por supuesto, porque el investigador principal del trabajo de biología se apellida Escudero.
Escarabajo con una muesca en forma de escudo (https://es.wikipedia.org/wiki/Escutoide#/media/File:Protaetia-cuprea-ignicollis-IZE-257.jpg )

Pues bien, uniéndose de este modo, las células epiteliales, además de rellenar completamente el espacio, minimizan su gasto de energía. Esas uniones, como vemos en la siguiente ilustración, no tienen por qué ser en planos rectos (descrito así por simplicidad), sino que suelen ser de forma curvada.
Por si todo esto fuera poco, entre los autores de este hallazgo se encuentra nuestra compañera, amiga y participante en varias charlas de divulgación de nuestro museo, Clara Grima (autora del blog “Mati y sus mateaventuras”). En este enlace puede leerse un estupendo y didáctico artículo escrito por ella misma sobre los escutoides, para quien desee profundizar un poco más en esta singular estructura.
No todos los días pueden describirse aplicaciones tan matemáticas que puedan explicarse a grandes rasgos (bueno, ésta tiene más fundamento matemático detrás: los diagramas de Voronoi, que no se detallan por no alargar esta entrada), pero lo que sí encontramos diariamente son nuevos resultados matemáticos, que quizá algún día tengan también su aplicación práctica. Las matemáticas son probablemente, una de las disciplinas más fecundas que existen, y con cada nuevo descubrimiento, nuevas incógnitas y posibilidades de investigación surgen, en progresión casi geométrica. Una pequeña parte de su abanico de posibilidades la disfrutaremos pronto. En este Museo.
Alfonso J. Población
Dpto. de Matemática Aplicada
Universidad de Valladolid
Una nueva superficie: los escutoides
El pasado 27 de julio la revista Nature Communications publicaba un artículo con un gran impacto mediático internacional sobre la manera en la que el tejido epitelial (o epitelio) se organiza para conformar y recubrir las cavidades y las superficies estructurales del cuerpo de los animales a medida que éstos se van desarrollando. La imagen muestra un ejemplo de epitelio cilíndrico o columnar: (https://es.wikipedia.org/wiki/Epitelio#/media/File:Simple_columnar_epithelium_tissue.svg ) Lo excepcional del trabajo, aparentemente técnico a partir de esta descripción, radica, por una parte, en su
Una nueva superficie: los escutoides
El pasado 27 de julio la revista Nature Communications publicaba un artículo con un gran impacto mediático internacional sobre la manera en la que el tejido epitelial (o epitelio) se organiza para conformar y recubrir las cavidades y las superficies estructurales del cuerpo de los animales a medida que éstos se van desarrollando. La imagen muestra un ejemplo de epitelio cilíndrico o columnar: (https://es.wikipedia.org/wiki/Epitelio#/media/File:Simple_columnar_epithelium_tissue.svg ) Lo excepcional del trabajo, aparentemente técnico a partir de esta descripción, radica, por una parte, en su
No es veneno todo lo que parece
Las serpientes siempre han generado mucho miedo en las personas, a pesar de que muchas de ellas son inofensivas para el ser humano. En Valladolid encontramos seis especies de estos ofidios, cuatro de ellos terrestres y dos ligados al agua y zonas húmedas. Las serpientes, por norma general, no atacan a las personas y tampoco moran cerca de las viviendas. No obstante, los contactos son frecuentes y en muchos casos perniciosos para estos animales. En caso de toparnos con alguna y
Una mirada hacia la colmena
El avispón asiático, también conocido como Vespa velutina en el ámbito científico, es un himenóptero que suscita gran interés en la actualidad debido, en parte, a la creencia de tratarse de un animal muy peligroso. Esta especie nativa del sureste asiático está catalogada como exótica invasora y, si bien es cierto que no hay que temer especialmente por la peligrosidad de su picadura, sí genera ciertos problemas ecológicos derivados de su presencia. Pero, ¿por qué es dañino el avispón asiático? Por un
¿Qué observar en el cielo durante el mes de agosto?
Durante el mes de agosto, el triángulo de verano se localiza sin ningún problema en la parte más alta del cielo donde, recordamos, se puede observar la preciosa estrella doble Albireo (constelación del Cisne). Además, si nos encontramos en un lugar oscuro, o al menos todo lo oscuro que podamos, podemos observar la siempre majestuosa Vía Láctea, pasando por la mitad de este triángulo. En cuanto a planetas, Venus es visible al atardecer hacia el Oeste e irá poco a poco
Cazadores aéreos, similares, pero no iguales
Los largos y calurosos días de verano no suelen ser buenos para la observación ornitológica. Al igual que las personas, las aves suelen limitar sus periodos de mayor actividad a las primeras y últimas horas de la jornada, cuando las temperaturas dan un respiro. Las golondrinas, aviones y vencejos son aves que solemos asociar al verano, ya que su vinculación a los núcleos de población y sus vuelos cercanos y constantes las hacen fácilmente reconocibles. Sin embargo, en muchas ocasiones





